Logika Automated Reasoning for Conditionals

There are three key points to understand about how Logika automated deduction deals with if statements:

  • checking the test expression: when Logika encounters an if statement, it will using a summoning of the SMT solvers to see, based on the known facts at that point, if it can determine if the if test expression is true or false. If the summoning identicates that the test expression is true or false, Logika will process the corresponding branch. The more common case is that it cannot determine whether the test expression is true or not, and in this case Logika processes both branches of the if statement.
  • checking each branch, with expanded knowledge about the test expression: as Logika descends into a branch of a if, it will add to its known facts the logical condition that must be true for control to flow into that branch. For example, in the max example above, upon entering the true branch, Logika will record in its known facts x > y, i.e., the test expression of the if statement holds within the true branch. When entering the false branch, Logika indicates in the known facts that the test expression is false, i.e., !(x > y)
  • merging knowledge of both branches when the if statement is complete: when Logika is unable to decide the test expression and has to explore both true and false branches, at the completion of the if Logika must merge facts from both branches while keeping track of which branch the facts apply to. It does this facts that are conditioned on the value of the test expression, e.g., from the true branch, it will keep the fact (x > y) ->: (max == x) after the conditional completes.

We now illustrate how this process is reflected in the IVE.

First, consider the known facts at the top of the loop at Line 8 (before the test expression is evaluated).

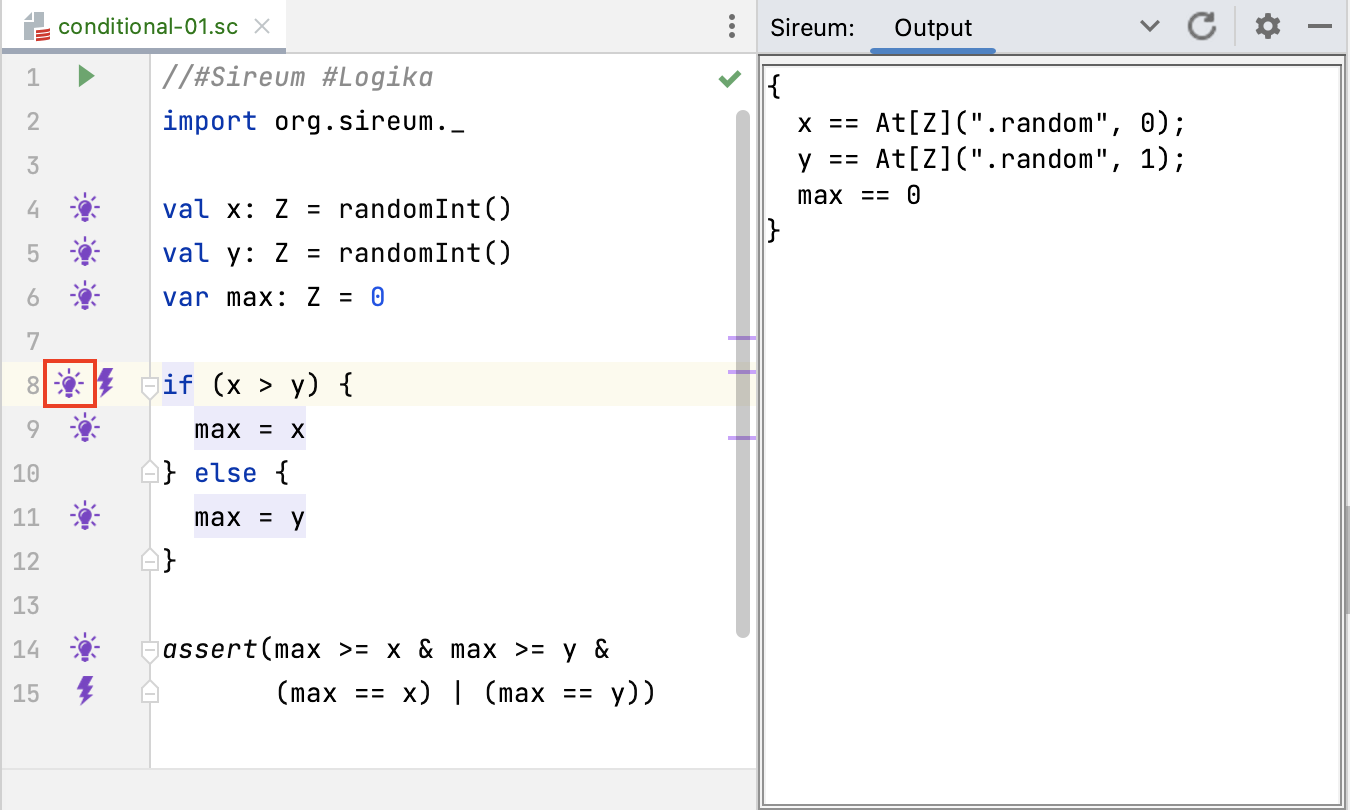
Logika - Conditionals Reasoning Before If

Here, we see only the basic facts about the variables x,y, and z. In particular, since x and y are unconstrained, Logika is unable to determine if the test expression x > y is true or false. Therefore, it will explore both branches (and we can see that since lightbulb annotations appear in both branches at Line 9 and Line 11).

Now consider the known facts as we enter the true branch at Line 9. Since we are inside the true branch, we are dealing with the case where the test expression must be true, and so Logika adds x > y to the known facts, as illustrated below.

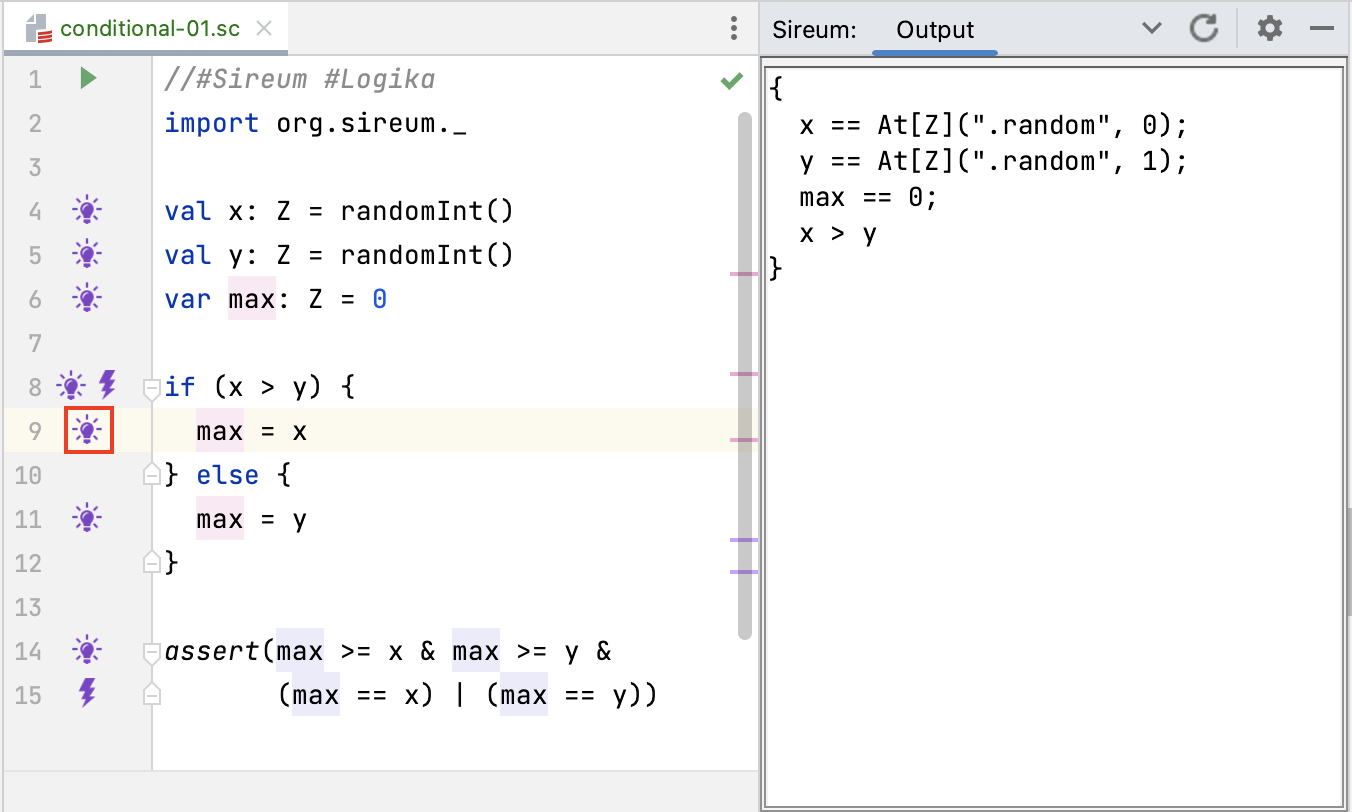
Logika - Conditionals Reasoning Before If

On the other hand, the following screen shot shows the known facts at Line 11 as Logika explores the false branch – !(x > y) has been added to the known facts, indicating that the test expression is false.

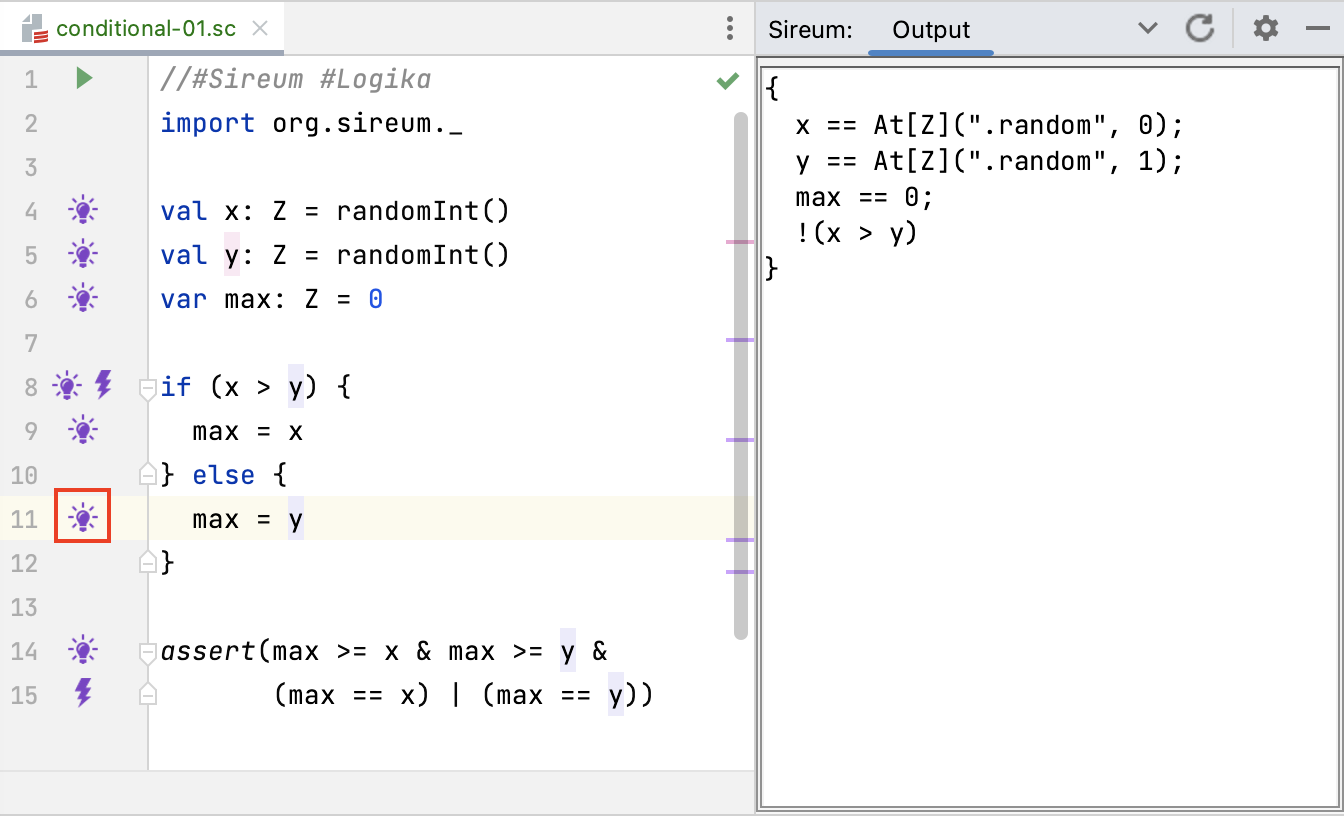
Logika - Conditionals Reasoning Before If

After the conclusion of the if statement, the known facts at Line 14 show Logika has merged the knowledge from both branches: the facts originating in each branch of the if are now conditioned (using implication ->:) on the value of the test expression within the respective branch.

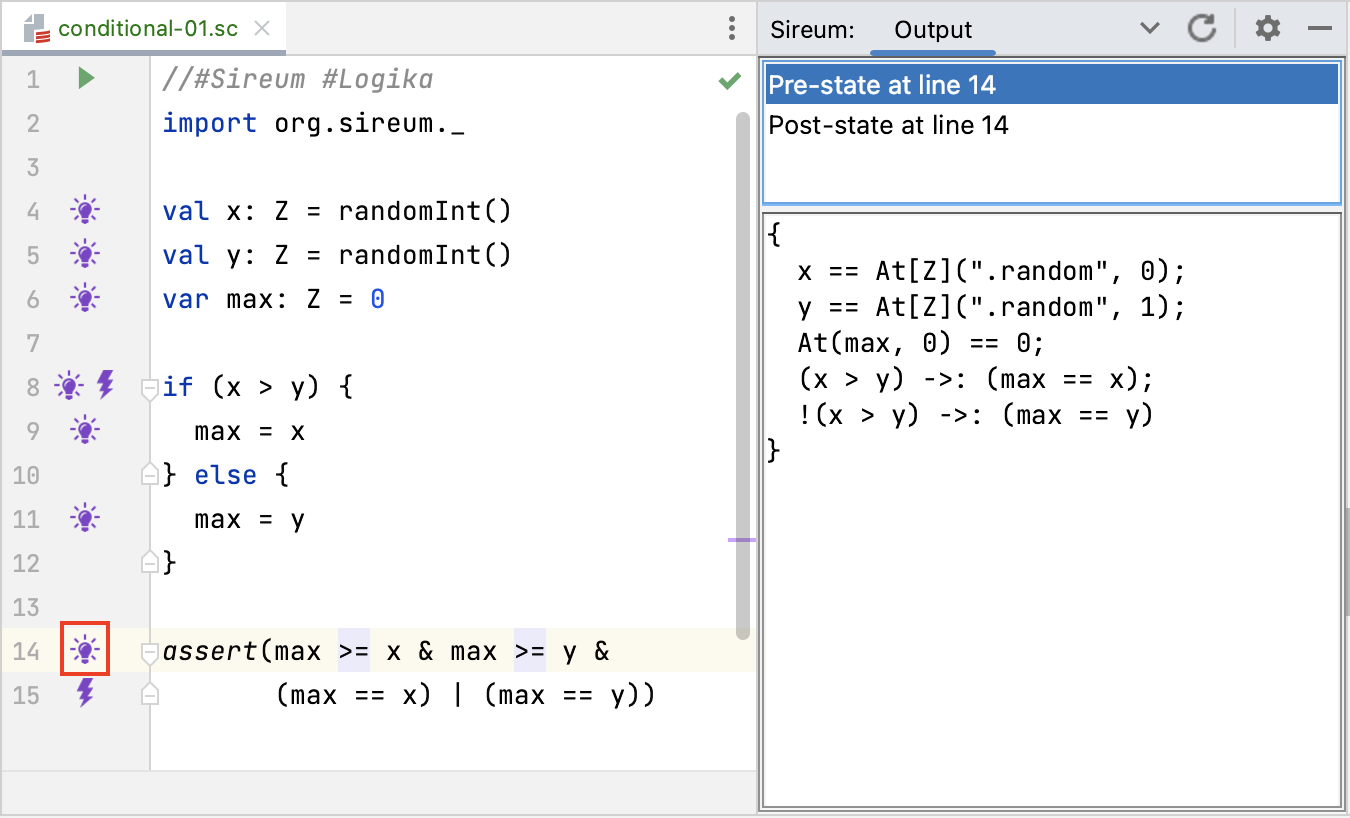
Logika - Conditionals Reasoning Before If

The aggregated known facts at this point are sufficient for the SMT solvers to prove that assertion at Line 14 hold, which captures the correctness property of the “find max” calculation.

Overview of Conditional Statements

In this chapter, we begin by considering how the meaning of conditional statements with the structure below can be captured in terms of facts.

1
2
3
4
5

if (B) {  // B is a boolean expression
  S       // S is a (possibly composite) Slang command
} else {
  T       // T is a (possibly composite) Slang command
}

The intuition of conditional executed is easily stated:

  • The test expression B is evaluated to obtain some boolean value b,
  • If b is true, then true branch S is executed and the false branch T is bypassed,
  • If the condition b is false, then the false branch T is executed and the true branch S is bypassed.

This is our first example of a control command: a command whose execution will select a path of future commands to execute from among several possible paths. In this case, the outcome of evaluating the test expression B will determine whether or not the path through S or the path through T is executed. We also refer to S and T as the branches of the conditional.

Control statements are interesting when considering the task of discovering the meaning of a program because we need to discover the meaning along all possible paths associated with the control statement. In a conditional statement, we only have two paths, but in a while statement, for instance, we can have a possibly infinite number of paths.

This impacts logic-based reasoning because we often need to form facts that summarize the meaning of the control statement across all of its possible paths. It impacts testing because we typically need to design our tests to cover as many paths through the control statement as is reasonable with respect to our testing objectives.

Further complicating matters is that control statements may appear to have paths in their static structure that will never be reached during execution. Consider the very simple conditional statement below. Because x has the value 10, the test expression x < 4 will always evaluate to false and so the true branch y = y + 1 is infeasible – there is no execution scenario in which it will be executed.

1
2
3
4
5
6
7

var y = 100
val x = 10
if (x < 4) {
  y = y + 1    // an infeasible branch (dead code)
} else {
  y = y - 1
}

Code that will never be executed on any trace through the program is sometimes called “dead code”.
Although dead code is not necessarily “faulty”, in many verification regimes, it is considered problematic because it is often an indication that the developer has made some sort of logic mistake: why should you write a block of code that will never be executed? Thus, verification regimes for safety-critical software often have a requirement that software should contain no dead code. This is an example of a software requirement that cannot be translated directly into a logical specification (e.g., an assertion), but we still need to find some way to apply our verification techniques (whether logic-based formal methods or testing) to produce evidence that the requirement is satisfied.

Example

To motivate how we can systematically reason about conditional statements, consider the following example that finds the maximum value of two variables x and y. Our explanation does not rely on the declarations of x and y and so we omit them for now.

1
2
3
4
5
6
7

var max: Z = 0
// deduce max == 0      (statement fact: assignment)
if (x < y) {
  max = y
} else {
  max = x
}

We start off by deducing a fact about the value of max based on the principles introduced in the previous chapter. We know that the test expression x < y is evaluated next. However, for this program, it is impossible to predict the value of the test expression during static verification, because we have no facts about x and y. Therefore, it is impossible for us to predict whether the true branch or the false branch will be executed. Consequently, we must analyze both branches to ensure that we discover the complete meaning of the code.

Previously deduced facts can be carried down into branches: Since the test of the conditional is an expression, we know its evaluation will not update any variables. Therefore, any facts that are true immediately before the conditional such as z == 0 can be carried down into both branches.

1
2
3
4
5
6
7
8
9

var max: Z = 0
// deduce max == 0      (statement fact: assignment)
if (x < y) {
  // deduce max == 0    (previously deduced fact) 
  max = y
} else {
  // deduce max == 0    (previously deduced fact)  
  max = x
}

As an aside, languages like C allow expressions to have side-effects (e.g., x++). However, using those features generally complicate reasoning. Using such expressions in conditional tests prevents one from applying universally the “facts carry over into the braches” reasoning above since an expression like x++ could possibly invalidate facts containing x.

Picking up knowledge from test evaluation: Although we cannot predict the exact value for the test expression x < y, we do know that if execution ends up in the true branch, it must be the case that x < y holds. Conversely, if execution ends up in the false branch, we know that !(x < y) holds. These facts follow immediately from the structure of a conditional, so we label them as statement facts.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

var max: Z = 0
// deduce max == 0      (statement fact: assignment)
if (x < y) {
  // deduce max == 0    (previously deduced fact) 
  // deduce (x < y)     (statement fact: conditional-true)
  max = y
} else {
  // deduce max == 0    (previously deduced fact)  
  // deduce !(x < y)    (statement fact: conditional-false)
  max = x
}

Reasoning about individual branches: In each branch, we simply apply our existing reasoning principles. We’ll see later than if we aim for certain facts, reasoning can be simplified a bit. For now, let’s just capture the consequences of the assignment to max in both branches.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

var max: Z = 0
// deduce max == 0      (statement fact: assignment)
if (x < y) {
  // deduce max == 0    (previously deduced fact) 
  // deduce (x < y)     (statement fact: conditional-true)
  max = y
  // deduce At(max,0) == 0  (previously deduced fact)
  // deduce max == y        (statement fact: assignment)
} else {
  // deduce max == 0    (previously deduced fact)  
  // deduce !(x < y)    (statement fact: conditional-false)
  max = x
  // deduce At(max,0) == 0  (previously deduced fact)
  // deduce max == x        (statement fact: assignment)
}

We can carry over the fact related to the initial value of max (taking care to understand that we are now referencing a previous version). Then, in both branches we can deduce a new value for max.

Merging facts at the end of a conditional: The end of a conditional is a situation where multiple paths through the code (two in this case – for the true and false branches) join to execute a common set of commands (the code immediately after a conditional). Similar (and even more complicated) situations exist at the conclusion of a loop. It is possible to continue on with two distinct reasoning activities at the end of a conditional: one carrying along the facts from the true branch and another carrying along facts from the false branch. While some automated analysis tools work this way (e.g., some tools typically classified as model checkers), this strategy has the disadvantage that there can be a combinatorial explosion of paths to consider (e.g., when the code has multiple conditional statements in a row). It’s more common for deductive tools designed for contract verification to try to derive facts at the point of path merging that summarize and combine the earlier facts from the individual paths. One natural approach is to combine facts from merged branches with disjunction, as illustrated below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

var max: Z = 0
// deduce max == 0      (statement fact: assignment)
if (x < y) {
  // deduce max == 0    (previously deduced fact) 
  // deduce (x < y)     (statement fact: conditional-true)
  max = y
  // deduce At(max,0) == 0  (previously deduced fact) 
  // deduce (x < y)         (previously deduced fact) 
  // deduce max == y        (statement fact: assignment)
} else {
  // deduce max == 0    (previously deduced fact)  
  // deduce !(x < y)    (statement fact: conditional-false)
  max = x
  // deduce At(max,0) == 0  (previously deduced fact)
  // deduce !(x < y)        (previously deduced fact) 
  // deduce max == x        (statement fact: assignment)
}
//  deduce   (At(max,0) == 0 & (x < y) & max == y) 
           | (At(max,0) == 0 & !(x < y) & max == x)   (conditional fact merge)

The intuition here is that at the bottom of the conditional, we cannot statically predict which branch was taken, but we can say that either the facts from the end of the true branch hold or the facts from the end of the false branch hold. The presence of conditional expression facts (x < y) and !(x < y) in each side of the disjunction allow is to associate each disjunct with either the true branch or false branch.

There are additional strategies possible for reasoning about the merging. First, note that when one has a fact that appears at the end of both branches (i.e., it is “common” to both branches), then the fact is guaranteed to hold at the end of the conditional regardless of which branch is executed. Abstractly, the following reasoning principle holds for fact f.

1
2
3
4
5
6
7
8

if (B) {
  S
  // deduce f
} else {
  T
  // deduce f
}
// deduce f      (conditional fact merge: common)

Note that applying the first merging principle would give f | f, which simplifies to f, to give what we have written immediately above.

Applying this principle to the constraint At(max,0) == 0 which appears in both branches of the conditional, we can rearrange the deduce annotations at the conclusion of the conditional to be

//  deduce   At(max,0) == 0 
//  deduce   (x < y) & max == y | !(x < y) & max == x

Intuitively, last fact above is indicating that max == y is associated with the true branch and max == x is associated with the false branch. Because we know that (x < y) | !(x < y) always holds (law of the excluded middle), it is sound to restate the concluding deduces as

//  deduce   At(max,0) == 0 
//  deduce   (x < y) ->: max == y & !(x < y) ->: max == x

where ->: is Slang’s syntax for implication. We can also break conjuncts out into separate the deduce annotations.

//  deduce   At(max,0) == 0          (conditional fact merge: common)
//  deduce   (x < y) ->: max == y    (conditional fact merge: true branch)
//  deduce   !(x < y) ->: max == x   (conditional fact merge: false branch)

Logika uses this last strategy for merging.

Reasoning Schema

Consider the outline of a conditional statement below

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

// deduce f        // some fact that is deducible immediately before the conditional 
if (B) {
  // deduce B      (statement fact: conditional true)
  // deduce f      (previously deduced fact)
  S
  // deduce f-t
} else {
  // deduce !B     (statement fact: conditional false)
  // deduce f      (previously deduced fact)
  T 
  // deduce f-f
}

Execution of Conditionals

Of course, we understand the meaning of a conditional

1
2
3
4
5

if (B) {
  S
} else {
  T
}

Understanding the execution of a conditional precisely, we can also reason about it. We want to reason about the effect of the conditional without executing it.

Reasoning about Conditionals

We know that S or T is executed depending on the value of B

1
2
3
4
5

if (B) {
  S
} else {
  T
}

This means,

  • When first branch is entered, B becomes initially a fact in that branch
  • When second branch is entered, !B becomes initially a fact in that branch
1
2
3
4
5
6

if (B) {
  // deduce B
  S
} else {
  T // deduce !B
}

Example: Computing the Maximum of two Integers

Example A: Computing the Maximum

As an example of a program with a conditional, we use the program for computing the maximum of two integers below.

We focus on the highlighted fragment on the following slides assuming variables x and y and ignoring the final assertions for now.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

// #Sireum #Logika
import org.sireum._
val x: z = randomInt()
val y: z = random Int()

var z: Z = 0
if (x < y) {
    z = y
} else {
    z = x
}
assert(z == x | z == y)
assert(y <= z & x <= z)

The assignment var z: Z = 0 yields the fact z == 0

Reason about Conditionals (Completed)

We can complete our method for reasoning about conditionals now:

  • When first branch is entered, B becomes initially a fact in that branch
  • When second branch is entered, !B becomes initially a fact in that branch
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

if (B) {
    // deduce B
    S
    // ... deduce C
} else {
    // deduce !B
    T
    // ... deduce D
}
// deduce C | D
  • If we can deduce some fact C at the end of the first and a fact D at the end of the second branch, then we deduce C | D after the conditional.

Reason about Conditionals (Completed Special Case)

We can complete our method for reasoning about conditionals now:

  • When first branch is entered, B becomes initially a fact in that branch
  • When second branch is entered, !B becomes initially a fact in that branch
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

if (B) {
    // deduce B
    S
    // ... deduce C
} else {
    // deduce !B
    T
    // ... deduce D
}
// deduce C
  • If we can deduce some fact C at the end of the first and the second branch, then we deduce C after the conditional (because C | C is identical to C)

Exercise

Implement and verify a program computing the absolute value of an integer using Slang deductions according to the contract below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

// #Sireum #Logika
import org.sireum._
val x: Z = randomInt()
val y: Z = randomtInt()
__________________
__________________
__________________
__________________
__________________
__________________
__________________
__________________
assert(x/y == 1 | x/y == -1)
assert(y >= 0)

Example B: Biased Difference

Let’s consider a small variation of the maximum program

1
2
3
4
5
6
7
8

var z: Z = 0
if (x < y) {
  z = y
} else {
  z = x
}
z = z - x
assert(z == 0 | z = y - x)

It has an additional assignment at the end. We can reuse the deductions from the maximum problem, only dealing with the added assignment. We already know the deductions we can make at the end of the conditional.

1
2
3
4
5
6
7
8
9

var z: Z = 0
if (x < y) {
  z = y
} else {
  z = x
}
// deduce z == x | z == y
z = z - x
assert(z == 0 | z = y - x)

Of course, the assignment z = z - x changes this fact.

We can deduce At(z, 1) == z + x and replace At(z, 1) in the disjunction.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

var z: Z = 0
if (x < y) {
  z = y
} else {
  z = x
}
// deduce z == x | z == y
z = z - x
// deduce At(z, 1) == x | At(z, 1) == y
// deduce z == At(z, 1) - x
assert(z == 0 | z == y - x)

This gives the new fact z + x == x | z + x == y.

We already know the deductions we can make at the end of the conditional.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

var z: Z = 0
if (x < y) {
  z = y
} else {
  z = x
}
// deduce z == x | z == y
z = z - x
// deduce At(z, 1) == x | At(z, 1) == y
// deduce z == At(z, 1) - x
// deduce z + x == x | z + x == y
assert(z == 0 | z == y - x)

The assertion now holds by simple algebra.

Example B: Biased Difference Program in Logika

Biased_Diff_1 The deductions and final assertions are verified by Logika.

Programs are Facts

Programs with conditionals correspond to facts of the shape (B -> Sfact) & (!B -> Tfact)

1
2
3
4
5

if (B) {
    S
} else {
    T
}

A little complication will appear later with respect to replacing “old variables” in Sfact and Tfact. Aside. We can also write the conjunction (B -> Sfact) & (!B -> Tfact) as the equivalent disjunction (B & Sfact) | (!B & Tfact). In Logika the first form is used. It permits writing larger formulas in tabular e.g., when dealing with nested conditionals.

Verifying the Maximum Program in Logika

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

\begin{lstlisting}[escapechar=~]
// #Sireum #Logika
import org.sireum._
val x: Z = randomInt()
val y: Z = randomInt()

var z: Z = 0
if (x < y) {
  Deduce(|- (x < y))
  Deduce(|- (x <= y))
  z = y
  Deduce(|- (x <= z))
  Deduce(|- (z == y))
} else {
  Deduce(|- (!(x < y)))
  Deduce(|- (y <= x))
  z = x
  Deduce(|- (y <= z))
  Deduce(|- (z == x))
}
assert(z == x | z == y)
assert(y <= z & x <= z)

We have added some Deduce commands to the program to document why it works. If all Deduce commands are removed, Logika verifies the program fully automatic. In the future, we will only state facts relevant for the understanding, leaving to Logika some of the work and relying on the reader to fill in the gaps.

The Maximum Program in Logika

Maximum_1 Facts known after the first assignment to z. Maximum_2 Facts known when entering the first branch. Maximum_3 Facts known after the assignment to z in the first branch. Maximum_4 Facts known when entering the second branch. Maximum_5 Facts known after the assignment to z in the second branch. Maximum_6 Facts known after the conditional.

Nested Conditionals

The Maximum of Three Integers

The following program computes the maximum of three integers.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

if (x < y) {
  if (y < z) {
    m = z
  } else {
    m = y
  }
} else {
  if (x < z) {
    m = z
  } else {
    m = x
  }
}
assert(m == x | m == y | m == z)
assert(x <= m & y <= m & z <= m)

Exercise A: Add the facts that are initially true in each branch. Exercise B: Implement a program that chooses the maximum of four numbers.

The Program as a Fact

Programs with conditionals correspond to facts of the shape (B -> Sfact) & (!B -> Tfact).

1
2
3
4
5

if (B) {
    S
} else {
    T
}

We have the following law relating conjunction and implication: A -> (B -> C) is identical to (A & B) -> C. Thus, we have two equivalent ways to stack conditions as we move through nested conditionals. Let’s look directly at the way this is represented in Logika.

The Program in Logika

Nested-1 Facts following nested conditionals. The conditions are stacked horizontally reaching the inner blocks and vertically enumerating all blocks of the conditional.

The Maximum of Three Integers

Facts corresponding to the program with nested conditionals.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

if (x < y) {
  if (y < z) {
    m = z        // deduce   x < y  &   y < z  -> m == z
  } else {
    m = y        // deduce   x < y  & !(y < z) -> m == y
  }
} else {
  if (x < z) {
    m = z        // deduce !(x < y) &   x < z  -> m == z
  } else {
    m = x        // deduce !(x < y) & !(x < z) -> m == x
  }
}
// The facts are as seen from here

Each deduction is an implication C-> Bfact where C contains the conditions leading to block B and Bfact is the fact corresponding to that block.

The conjunction of these deductions is the fact corresponding to the program. Thus, we can easily relate the components of a Slang conditional P to the components of the corresponding fact Pfact

Example: Swapping two Integers

Blocks with Several Assignments

We have considered nested conditionals and seen that there is a close correspondence between programs and the deduced facts at all program locations. We look at a program with larger blocks next. Once we’ve observed these two variations it is not difficult to analyse more complex programs containing conditionals.

Example: Swapping two Integers

The following program chooses to use a local variable if x >= y

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

// #Sireum #Logika
import org.sireum._

val m: Z = randomInt()
val n: Z = randomInt()
var x: Z = m
var y: Z = n

if (x < y) {
  x = x + y
  y = x - y
  x = x - y
} else {
  val t = x
  x = y
  y = t
}
assert(x == n & y == m)

The Example in Logika

Swap_choice_1 Note that the local variable t is only used in the “past form”" At(t, 0). This variable is not available in the “present form” after the block. Swap_Block_1 This is a property of local variables in block.

Exercise

Is the following program correct? Why? Add Slang deductions to document your argument

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

// #Sireum #Logika
import org.sireum._

var a: B = randomInt() > 0
var b: B = randomInt() > 0

if (!a || b) {
  a = !a
} else {
  a = !b
}
assert(a | b)

Symbolic Execution

Facts as Values in Conditionals

Recall the maximum program:

1
2
3
4
5
6
7

var z: Z = 0
if (x < y) {
  z = y
} else {
  z = x
}
assert(z == x | z == y)

Symbolic execution of conditionals collects the conditions and their negations in different paths described by the corresponding path conditions. This corresponds closely to the way conditions are stacked when considering conditionals as facts.

Using Facts as Values

1
2
3
4
5
6
7

var z: Z = 0
if (x < y) {
  z = y
} else {
  z = x
}
assert(z == x | z == y)
  • Executing var z: Z = 0 yields (x: X, y: Y, z: 0), (PC: true)
  • Executing if (x < y) yields (x: X, x: X, z = 0), (PC: X < Y)
  • Executing z = y yields (x: X, y: Y, z: Y), (PC: X < Y)
  • Executing assert(...) yields (x: X, y: Y, z: Y), (PC: X < Y, Y == X | Y == Y)
  • Executing else yields (x: X, x: X, z: 0), (PC: !(X < Y))
  • Executing z = x yields (x: X, y: Y, z: X), (PC: !(X < Y))
  • Executing assert(...) yields (x: X, x: X, z: X), (PC: !(X < Y), X == X | X == Y)

Execution Tree

The two possible outcomes of a condition like x < y give rise to a tree structure of a symbolic execution.

flowchart TB
    A[(.., z: 0), (PC: true)]
    A --> B[(...,z: 0), (PC: X < Y)]
    A -- C[(...,z: 0), (PC:!( X < Y))]
    B -- D[(...,z: Y), (PC: X < Y)]
    C -- E[(...,z: X), (PC:!( X < Y))]
. . , , z z : : 0 Y ) ) , , ( ( P P C C : : X X . , < < z Y Y : ) ) 0 ) , ( P C : t r u . . e , , ) z z : : 0 X ) ) , , ( ( P P C C : : ! ! ( ( X X < < Y Y ) ) ) )

(Some information has been omitted from the tree to keep it readable)

Slang Examples

Absvalue nn

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

// #Sireum #Logika
import org.sireum._
val x: Z = randomInt()
var y: Z = randomInt()

assume(x != 0)
if (x < 0) {
  y = -x
} else {
  y = x
}

assert(x/y == 1 | x/y == -1)
assert(y >= 0)

Boolor

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

// #Sireum #Logika
import org.sireum._

var a: B = randomInt() > 0
var b: B = randomInt() > 0

if (!a || b) {
  a = !a
} else {
  a = !b
}
assert(a | b)

Maximum Diff

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

// #Sireum #Logika
import org.sireum._
val x: Z = randomInt()
val y: Z = randomInt()

var z: Z = 0
if (x < y) {
  z = y
} else {
  z = x
}
z = z - x
assert(z == 0 | z == y - x)

Maximum Diff Ded

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

// #Sireum #Logika
import org.sireum._
val x: Z = randomInt()
val y: Z = randomInt()

var z: Z = 0
if (x < y) {
  z = y
} else {
  z = x
}
Deduce(|- (z == x | z == y))
z = z - x
Deduce(|- (At(z, 1) == x | At(z, 1) == y))
Deduce(|- (z == At(z, 1) - x))
Deduce(|- (z + x == x | z + x == y))
assert(z == 0 | z == y - x)

Maximum Simple

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

// #Sireum #Logika
import org.sireum._
val x: Z = randomInt()
val y: Z = randomInt()

var z: Z = 0
if (x < y) {
  z = y
} else {
  z = x
}
assert(z == x | z == y)
assert(y <= z & x <= z)

Maximum Simple Ded

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

// #Sireum #Logika
import org.sireum._
val x: Z = randomInt()
val y: Z = randomInt()

var z: Z = 0
if (x < y) {
  Deduce(|- (x < y))
  Deduce(|- (x <= y))
  z = y
  Deduce(|- (x <= z))
  Deduce(|- (z == y))
} else {
  Deduce(|- (!(x < y)))
  Deduce(|- (y <= x))
  z = x
  Deduce(|- (y <= z))
  Deduce(|- (z == x))
}
assert(z == x | z == y)
assert(y <= z & x <= z)

Nested Max

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

// #Sireum #Logika
import org.sireum._
val x: Z = randomInt(); val y: Z = randomInt(); val z: Z = randomInt()
var m: Z = 0

if (x < y) {
  if (y < z) {
    m = z
  } else {
    m = y
  }
} else {
  if (x < z) {
    m = z
  } else {
    m = x
  }
}

assert(m == x | m == y | m == z)
assert(x <= m & y <= m & z <= m)

Swap Block

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

// #Sireum #Logika
import org.sireum._

val m: Z = randomInt()
val n: Z = randomInt()
var x: Z = m
var y: Z = n

{
  val t = x
  x = y
  y = t
}

assert(x == n & y == m)

Swap Choice

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

// #Sireum #Logika
import org.sireum._

val m: Z = randomInt()
val n: Z = randomInt()
var x: Z = m
var y: Z = n

if (x < y) {
  x = x + y
  y = x - y
  x = x - y
} else {
  val t = x
  x = y
  y = t
}
assert(x == n & y == m)

Summary

We have looked at conditionals:

  • by tracing facts through programs
  • by considering programs as facts
  • by symbolic execution

(Just as we did last week for assignments and compositions of assignments) We have reasoned about conditionals observing, in particular, the role of the conditions.