Lecture Summary: Contracts Test

Slang Functions

Example A: Pure Maximum Function

1
2
3
4
5
6
7


def max(x: Z, y: Z): Z = {
  if (x < y) {
    return y
  } else {
    return x
  }
}

Functions consist of a signature def max(x: Z, y: Z): Z and a body { ... }. The signature specifies the number of parameters, their type and the return type. The body contains the implementation code. Functions that do not return a value can also be defined def fun(x: Z, y: Z) { ... }.

1
2
3
4
5
6
7


@pure def pure_max(x: Z, y: Z): Z = {
  if (x < y) {
    return y
  } else {
    return x
  }
}

The body of function max only refers to the function parameters. Such functions are called pure. The @pure attribute indicates to Logika that the function is free of side-effects. When a contract is added it can be used in deductions like any other mathematical operator, e.g., + or <. Let’s have a look at contracts.

Example A: Pure Maximum Function Contract

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


@pure def pure_max(x: Z, y: Z): Z = {




  if (x < y) {
    return y
  } else {
    return x
  }
}

Contracts specify what’s required before the function is executed and what’s ensured after the function has been executed. Let’s state this informally.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


@pure def pure_max(x: Z, y: Z): Z = {
  // contract
  //   requires pre-condition
  //   ensures post-condition

  if (x < y) {
    return y
  } else {
    return x
  }
}

What’s required is called the pre-condition of the function. What’s ensured is called the post-condition of the function. We have already sketched such contracts using assume-assert.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


@pure def pure_max(x: Z, y: Z): Z = {
  // contract
  //   requires x > 0, y > 0
  //   ensures Res == x | Res == y, x <= Res, y <= Res

  if (x < y) {
    return y
  } else {
    return x
  }
}

It looked similar to this, reading , in the contract clauses as conjunctions. What’s new is the reference to Res in the ensures clause. The special variable Res is needed to deal with return statement.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


@pure def pure_max(x: Z, y: Z): Z = {
  // contract
  //   requires x > 0, y > 0
  //   ensures Res == x | Res == y, x <= Res, y <= Res

  if (x < y) {
    return y  // Res = y
  } else {
    return x  // Res = x
  }
}

We can read return statements as assignments to Res as indicated in the comments. This makes it straightforward to relate the post-condition to the function body. In Slang syntax it looks as follows …

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


@pure def pure_max(x: Z, y: Z): Z = {
  Contract(
    Requires(x > 0, y > 0),
    Ensures(Res == x | Res == y, x <= Res, y <= Res)
  )
  if (x < y) {
    return y
  } else {
    return x
  }
}

Remember to read return statements as assignments to Res. Pure function pure_max with its contract can now be used in formulas. In some context we could write, e.g., Deduce(|- (z == max(x, y))).

Example B: Impure Maximum Function

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


var z: Z = randomInt()
def impure_max(x: Z, y: Z) {


  if (x < y) {
    z = y
  } else {
    z = x
  }
}

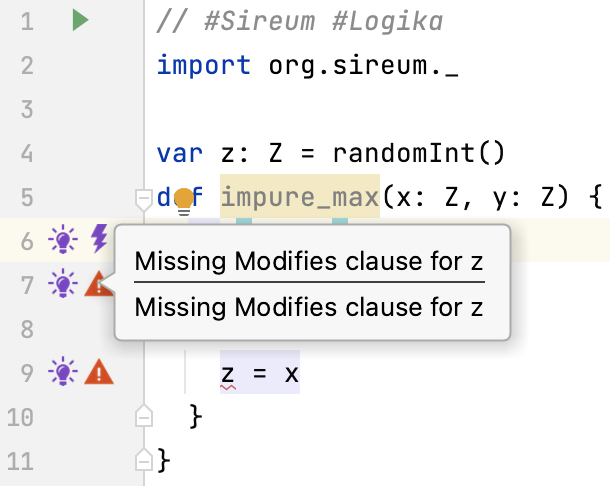
Function impure_max modified variable z outside its scope. It has the side-effect of modifying variable z. As opposed to function pure_max this function is impure. Logika rejects the program above. Missing_Modifies_Clause

Example B: Impure Maximum Function with Modifies Clause

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


var z: Z = randomInt()
def impure_max(x: Z, y: Z) {
  // contract
  //   modifies frame
  if (x < y) {
    z = y
  } else {
    z = x
  }
}

For impure functions the variables they modify outside their scope must be listed in the contract This is done by means of the modifies clause that specifies a function’s frame. A frame is a (comma-separated) list of variables.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


var z: Z = randomInt()
def impure_max(x: Z, y: Z) {
  // contract
  //   modifies z
  if (x < y) {
    z = y
  } else {
    z = x
  }
}

The frame of function impure_max is just the single variable z. We will discuss this more next week. For now we note that for a function with side-effects it is important to know which variables it might modify.

Fame of a Function

Consider a function with a contract.

1
2
3
4
5
6
7


var m: Z = randomInt()
var n: Z = randomInt()

def equalize(): Unit = {
  // contract
  //   ensures m == n
}

This could be achieved by assigning m to n, or n to m, or a common value to both. In general, the result of a function could be obtained by modifying variables that were intended as parameters. The modifies clause permits us to describe which variables might change and which do not.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


var z: Z = randomInt()
def impure_max(x: Z, y: Z) {
  Contract(
    Modifies(z)
  )
  if (x < y) {
    z = y
  } else {
    z = x
  }
}

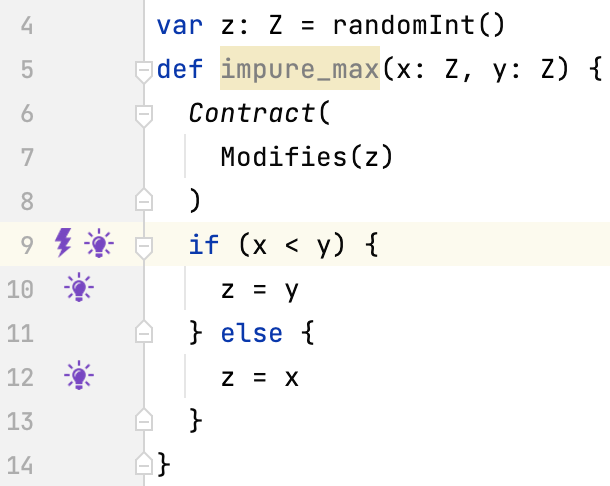
In the function above the frame is specified in the Slang contract notation. With the Modifies clause added Logika accepts the function. Inserted_Modifies_clause

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


var z: Z = randomInt()
def impure_max(x: Z, y: Z) {
  Contract(
    Requires(x > 0, y > 0),
    Modifies(z),
    Ensures(z == x | z == y, x <= z, y <= z)
  )
  if (x < y) {
    z = y
  } else {
    z = x
  }
}

Now we can specify the complete contract for the function. Note the use of variable z in place of Res in the pure version of the function.

Specification and Implementation

1
2
3
4
5
6
7
8


val x = randomInt()
assume(x > 0)
val y = randomInt()
assume(y > 0)

impure_max(x, y)

Deduce(|- (z == pure_max(x, y)))

We can now program with the impure function and use the pure function in correctness proofs. (Of course, we can also program with the pure function) Pure functions are often clearer but less efficient. They are good specifications. Impure functions are often more efficient but less clear. They are good implementations.

The fragment above proves that impure_max implements pure_max related by z == pure_max(x, y). We also say that impure_max refines pure_max. Note, the use of assume to constrain the values of x and y. assume is most useful to support proofs of the kind above.

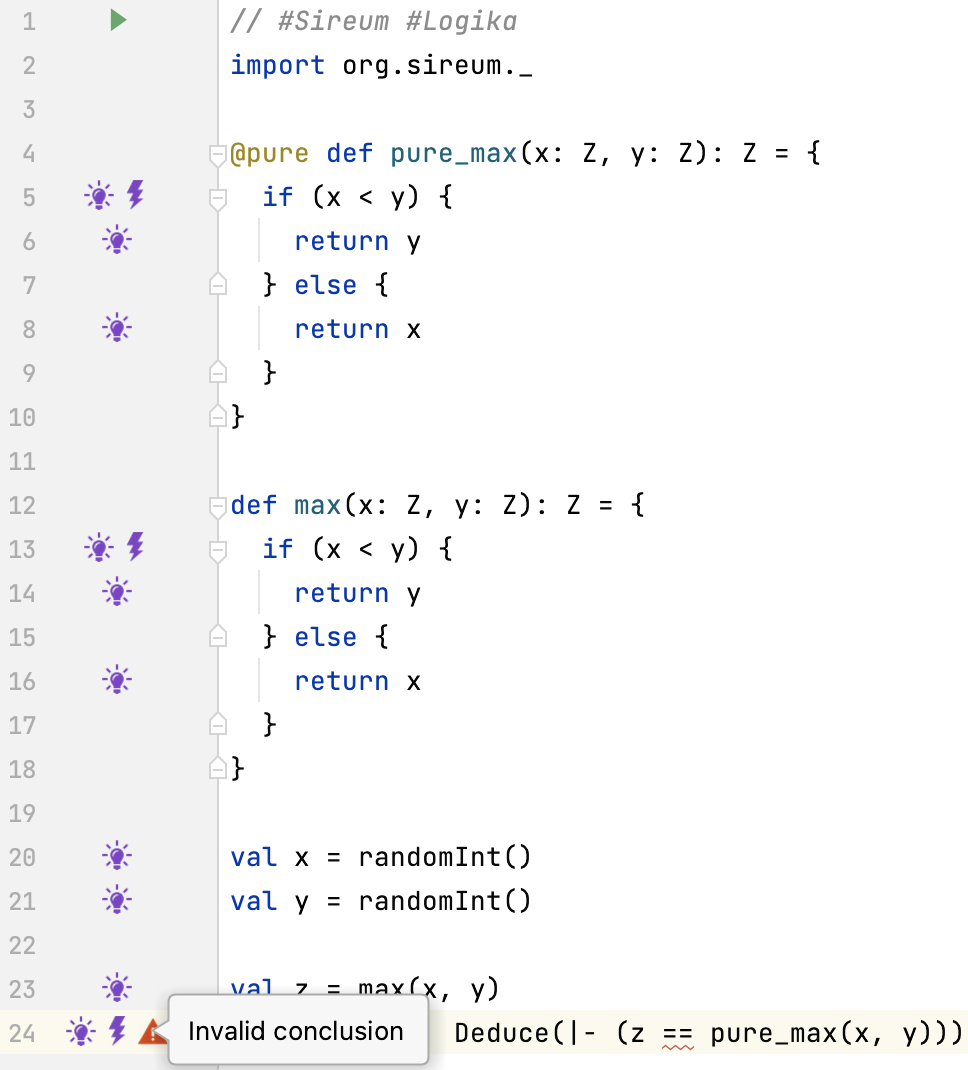
Exercise 1

Add contracts to functions max and pure_max so that the deduction at the end is verified. Exercise1

Testing with Contracts

Example C: Testing the Maximum Function

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


def max(x: Z, y: Z): Z = {
  Contract(
    Requires(x > 0, y > 0),
    Ensures(Res == x | Res == y, x <= Res, y <= Res)
  )
  if (x < y) {
    return y // "Res = y"
  } else {
    return x // "Res = x"
  }
}

Suppose the body of function max was more complex and we would have no proof that the body establishes the post-condition. We would like to have a method that helps us systematically to come up with test cases.

Test Cases from Specifications

def max(x: Z, y: Z): Z = {
  Contract(
    Requires(x > 0, y > 0),
    Ensures(Res == x | Res == y, x <= Res, y <= Res)
  )
}

We only consider the contract that specifies the behaviour of the function. The pre-condition restricts the values to be considered for the defined behaviour of the function. The post-condition describes possible outcomes depending on the input values:

If Res == x then y <= x
If Res == y then x <= y

Equivalence Partitioning

We can analyse the different in which y <= x and x <= y and their negations are conjoined to predict conditions occurring in an implementation.

1
2
3
4


 (y <= x) &  (x <= y) if and only if x == y
 (y <= x) & !(x <= y) if and only if x > y
!(y <= x) &  (x <= y) if and only if x < y
!(y <= x) & !(x <= y) if and only if false

We get three cases to consider: x < y, x == y, x > y. These are called equivalence classes.

Boundary Value Analysis

We can analyse pre-condition x > 0 and y > 0. They bound the possible values the parameters may take. The smallest value for x and y is 1. 1 is a boundary value for x and y. Aside. In some cases it is interesting to test the behaviour of a function when the pre-condition is violated, e.g., when security is a concern. We have collected equivalence classes and boundary values. These can be used to formulate test cases.

Test Case Formulation

Combining equivalence classes with boundary values we can calculate expected results.

Class	Input x	Input y	Output Res
x < y	1	2	2
x == y	1	1	1
x > y	2	1	2

The output Res must satisfy the condition Res == x | Res == y & x <= Res & y <= Res. Inserting the values for x and y from the table,Res can be calculated. Boundary values have been shown to be good choices for detecting faults in programs. The derivation of the test cases above is driven by heuristics of equivalence partitioning and boundary value analysis.

The test cases are not best choices but heuristically well chosen
The test cases might miss important faults in a program

Test Cases from Implementations

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


def max(x: Z, y: Z): Z = {
  Contract(
    Requires(x > 0, y > 0),
    Ensures(Res == x | Res == y, x <= Res, y <= Res)
  )
  if (x < y) {
    return y // "Res = y"
  } else {
    return x // "Res = x"
  }
}

Taking the body of function max we can make sure that all statements and conditions on all branches are tested. “all statements and conditions on all branches” is called a coverage criterion. Aside. Other coverage criteria exist (but we will not discuss them).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


def max(x: Z, y: Z): Z = {
  Contract(
    Requires(x > 0, y > 0),
    Ensures(Res == x | Res == y, x <= Res, y <= Res)
  )
  if (x < y) {
    return y // "Res = y"
  } else {
    return x // "Res = x"
  }
}

Let’s have a look at the fact corresponding to the program. The body has two branches that are followed depending on whether the condition x < y is true or false.

We derive test cases from the fact pre-condition & body_fact & (replacing ‘return e’ by ‘Res = e’ in body) post-condition For function max we get:

1
2
3
4


x > 0 & y > 0 &                              // Pre-condition
x < y => Res == y &                          // Branch 1
!(x < y) => Res == x &                       // Branch 2
(Res == x | Res == y) & x <= Res & y <= Res  // Post-condition

Conjoining either x < y or x >= y we force the choice between branch 1 and branch 2.

Two facts result, one for each branch.

Branch 1

1
2
3


x > 0 & y > 0 &                              // Pre-condition
x < y & Res == y &                           // Branch 1
(Res == x | Res == y) & x <= Res & y <= Res  // Post-condition

Branch 2

1
2
3


x > 0 & y > 0 &                              // Pre-condition
x >= y & Res == x &                          // Branch 2
(Res == x | Res == y) & x <= Res & y <= Res  // Post-condition

Our prior analysis of the specification suggested that it would be good to split x >= y into the cases x == y and x > y to be tested separately.

Branch 1

1
2
3


x > 0 & y > 0 &                              // Pre-condition
x < y & Res == y &                           // Branch 1
(Res == x | Res == y) & x <= Res & y <= Res  // Post-condition

Branch 2 (with x == y)

1
2
3


x > 0 & y > 0 &                              // Pre-condition
x >= y & Res == x &                          // Branch 2
(Res == x | Res == y) & x <= Res & y <= Res  // Post-condition

Branch 2 (with x > y)

1
2
3


x > 0 & y > 0 &                              // Pre-condition
x >= y & Res == x &                          // Branch 2
(Res == x | Res == y) & x <= Res & y <= Res  // Post-condition

Test Cases from Implementations (Using Boundary Values)

Branch 1: x == 1, y == 2

1
2
3


x > 0 & y > 0 &                              // Pre-condition
x < y & Res == y &                           // Branch 1
(Res == x | Res == y) & x <= Res & y <= Res  // Post-condition

Branch 2 (with x == y): x == 1, y == 1

1
2
3


x > 0 & y > 0 &                              // Pre-condition
x >= y & Res == x &                          // Branch 2
(Res == x | Res == y) & x <= Res & y <= Res  // Post-condition

Branch 2 (with x > y): x == 2, y == 1

1
2
3


x > 0 & y > 0 &                              // Pre-condition
x >= y & Res == x &                          // Branch 2
(Res == x | Res == y) & x <= Res & y <= Res  // Post-condition

Branch 1: x == 1, y == 2

1
2
3


1 > 0 & 2 > 0 &                              // Pre-condition
1 < 2 & Res == 2 &                           // Branch 1
(Res == 1 | Res == 2) & 1 <= Res & 2 <= Res  // Post-condition

Branch 2 (with x == y): x == 1, y == 1

1
2
3


1 > 0 & 1 > 0 &                              // Pre-condition
1 >= 1 & Res == 1 &                          // Branch 2
(Res == 1 | Res == 1) & 1 <= Res & 1 <= Res  // Post-condition

Branch 2 (with x > y): x == 2, y == 1

1
2
3


2 > 0 & 1 > 0 &                              // Pre-condition
2 >= 1 & Res == 2 &                          // Branch 2
(Res == 2 | Res == 1) & 2 <= Res & 1 <= Res  // Post-condition

Branch 1: x == 1, y == 2, Res == 2

1
2
3


1 > 0 & 2 > 0 &                              // Pre-condition
1 < 2 & Res == 2 &                           // Branch 1
(Res == 1 | Res == 2) & 1 <= Res & 2 <= Res  // Post-condition

Branch 2 (with x == y): x == 1, y == 1, Res == 1

1
2
3


1 > 0 & 1 > 0 &                              // Pre-condition
1 >= 1 & Res == 1 &                          // Branch 2
(Res == 1 | Res == 1) & 1 <= Res & 1 <= Res  // Post-condition

Branch 2 (with x > y): x == 2, y == 1, Res == 2

1
2
3


2 > 0 & 1 > 0 &                              // Pre-condition
2 >= 1 & Res == 2 &                          // Branch 2
(Res == 2 | Res == 1) & 2 <= Res & 1 <= Res  // Post-condition

Branch 1: x == 1, y == 2, Res == 2

1
2
3


1 > 0 & 2 > 0 &                              // Pre-condition
1 < 2 & 2 == 2 &                             // Branch 1
(2 == 1 | 2 == 2) & 1 <= 2 & 2 <= 2          // Post-condition

Branch 2 (with x == y): x == 1, y == 1, Res == 1

1
2
3


1 > 0 & 1 > 0 &                              // Pre-condition
1 >= 1 & 1 == 1 &                            // Branch 2
(1 == 1 | 1 == 1) & 1 <= 1 & 1 <= 1          // Post-condition

Branch 2 (with x > y): x == 2, y == 1, Res == 2

1
2
3


2 > 0 & 1 > 0 &                              // Pre-condition
2 >= 1 & 2 == 2 &                            // Branch 2
(2 == 2 | 2 == 1) & 2 <= 2 & 1 <= 2          // Post-condition

Branch 1

satisfied by test case
input: x == 1, y == 2
output: Res == 2

Branch 2

with x == y satisfied by test case
input: x == 1, y == 1
output: Ress == 1

Branch 2

with x > y satisfied by test case
input: x == 2, y == 1
output: Res == 2

Symbolic Execution

Symbolic Execution of the Function Branch 1

1
2
3
4
5
6
7


... Requires(x > 0, y > 0)
... Ensures(Res == x | Res == y, x <= Res, y <= Res)
if (x < y) {
  return y // "Res = y"
} else {
  return x // "Res = x"
}

Entering the function yields (x: X, y: Y, Res: RES), (PC: X > 0, Y > 0)
Executing if (x < y) { yields (x: X, x: X, Res: RES), (PC: X > 0, Y > 0, X < Y)
Executing return y // "Res = y" yields (x: X, y: Y, Res: Y), (PC: X > 0, Y > 0, X < Y)
Leaving the function yields (x: X, y: Y, Res: Y), (PC: X > 0, Y > 0, X < Y, Y == X | Y == Y, X <= Y, Y <= X)

Symbolic Execution of the Function Branch 2

1
2
3
4
5
6
7


... Requires(x > 0, y > 0)
... Ensures(Res == x | Res == y, x <= Res, y <= Res)
if (x < y) {
  return y // "Res = y"
} else {
  return x // "Res = x"
}

Entering the function yields (x: X, y: Y, Res: RES), (PC: X > 0, Y > 0)
Executing } else { yields (x: X, x: X, Res: RES), (PC: X > 0, Y > 0, X >= Y)
Executing return x // "Res = x" yields (x: X, y: Y, Res: X), (PC: X > 0, Y > 0, X >= Y)
Leaving the function yields (x: X, y: Y, Res: X), (PC: X > 0, Y > 0, X >= Y, X == X | X == Y, X <= X, Y <= X)

Result of the Symbolic Execution

Symbolic execution of function max produces the following two results.

(x: X, y: Y, Res: Y), (PC: X > 0, Y > 0, X < Y, Y == X | Y == Y, X <= Y, Y <= Y)
(x: X, y: Y, Res: X), (PC: X > 0, Y > 0, X >= Y, X == X | X == Y, X <= X, Y <= X)

We can state these as facts:

x == X, y == Y, Res == Y, X > 0 & Y > 0 & X < Y & (Y == X | Y == Y) & X <= Y & Y <= Y
x == X, y == Y, Res == X, X > 0 & Y > 0 & X >= Y & (X == X | X == Y) & X <= X & Y <= X

These facts are very similar to those we have seen when looking at programs as facts. The only differences are:

We use symbolic values X, Y, and Res
Res has been replaced by Y and X, respectively

In the second branch we can distinguish X == Y and X > Y as before.

Into the three remaining cases we can insert the boundary values we have determined before.

Test Case 1 input: x == X, y == Y, output: Res == Y, X > 0 & Y > 0 & X < Y & (Y == X | Y == Y) & X <= Y & Y <= Y
Test Case 2 input: x == X, y == Y, output: Res == X, X == Y, X > 0 & Y > 0 & X >= Y & (X == X | X == Y) & X <= X & Y <= X
Test Case 3 input: x == X, y == Y, output: Res == X, X > Y, X > 0 & Y > 0 & X >= Y & (X == X | X == Y) & X <= X & Y <= X

Exercise 2

Formally determine the test cases for the function below.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


var z: Z = 0
def max(x: Z, y: Z) {
  Contract(
    Requires(x > 0, y > 0),
    Modifies(z),
    Ensures(z == x | z == y, x <= z, y <= z)
  )
  if (x < y) {
    z = y
  } else {
    z = x
  }
}

Remember that this function has a side-effect.

Testing for Faults

Test Cases for Faults in Implementations

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


var x: Z = randomInt()
var y: Z = randomInt()

def tsq() {
  Contract(
    Modifies(x, y),
    Ensures(x >= 0, y >= 0)
  )
  x = x * x
  y = y + y
  if (x < y) {
    y = y - x
  } else {
    x = x - y
  }
}

Is the function above correct? No. Can we determine a test case confirming this? Invalid_Post-condition

Counterexamples from Implementations

We seek a counterexample showing that the post-condition does not hold. More formally, this is expressed, pre-condition & body_fact & (body does not contain a return statement!) !post-condition For function tsq we get:

1
2
3
4
5
6
7


At(x, 1) == At(x, 0) * At(x, 0) &                // First assignment
At(y, 1) == At(y, 0) + At(y, 0) &                // Second assignment
(At(x, 1) < At(y, 1)) -> (x == At(x, 1)) &       // Branch 1
(At(x, 1) < At(y, 1)) -> (y == At(y, 1) - x) &
!(At(x, 1) < At(y, 1)) -> (y == At(y, 1)) &      // Branch 2
!(At(x, 1) < At(y, 1)) -> (x == At(x, 1) - y) &
(x < 0 | y < 0)                                  // Negated post-condition

Let’s focus on the failing post-condition y >= 0, considering branch 1.

Test Cases for Faults in Implementations

1
2
3
4
5
6


At(x, 1) == At(x, 0) * At(x, 0) &                // First assignment
At(y, 1) == At(y, 0) + At(y, 0) &                // Second assignment
(At(x, 1) < At(y, 1)) &                          // Condition to enter branch 1
(At(x, 1) < At(y, 1)) -> (x == At(x, 1)) &       // Branch 1
(At(x, 1) < At(y, 1)) -> (y == At(y, 1) - x) &
y < 0                                            // Negated failing post-condition

This is unsatisfiable. We have:

At(x, 1) >= 0 and At(y, 1) > At(x, 1)
Therefor, At(y, 1) - At(x, 1) > 0

Let’s have a look at branch 2.

1
2
3
4
5
6


At(x, 1) == At(x, 0) * At(x, 0) &                // First assignment
At(y, 1) == At(y, 0) + At(y, 0) &                // Second assignment
!(At(x, 1) < At(y, 1)) &                         // Condition to enter branch 2
!(At(x, 1) < At(y, 1)) -> (y == At(y, 1)) &      // Branch 2
!(At(x, 1) < At(y, 1)) -> (x == At(x, 1) - y) &
y < 0                                            // Negated failing post-condition

We proceed as if y < 0 was a post-condition and apply the same methods as before. We find: At(x, 0) == 0, At(y, 0) == -1, y == -2. Failing test case:

input: x == 0, y == 0
output: y == ? // where ? must satisfy ? >= 0

Exercise 3

Use Symbolic execution for the calculation of the counterexample. Correct the function.

Exercises

Exercise 4

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


var x = randomInt()
var q = randomInt()

def shift(p: Z, y: Z, N: Z) {
  Contract(
    Requires(x * p + y * q == N),
    Modifies(x, q),
    Ensures(x * p + y * q == N)
  )
  x = x - y
  q = q - p
}

Correct and verify the function above
Find a counterexample first by calculation
Derive test cases for the function
What are input and output?
Considering the post-condition choose suitable equivalence classes and boundary values (Consider p == 0 and y == 0 for the uncorrected function)
How many test cases do you get?
Add deductions that explain that your function is correct

Exercise 5 (Outlook)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


// linmap yields a * x + b for any a, x, and b
def linmap(a: Z, x: Z, b: Z): Z = {
  ...
}

// given (x - b) % a == 0 revmap yields (x - b) / a for any a, x, and b
def revmap(a: Z, x: Z, b: Z): Z = {
  ...
}

// compose yields x for any a, x, and b
def compose(a: Z, x: Z, b: Z): Z = {
  ...
  var y: Z = linmap(a, x, b)
  y = ... // use function revmap
  return y
}

Add the contracts according to the comments preceding the functions. Add deductions that explain that your implementation is correct.

Slang Examples

Linear Combination Contract Test Fault

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


// #Sireum #Logika
import org.sireum._

var x = randomInt()
var q = randomInt()

def shift(p: Z, y: Z, N: Z) {
  Contract(
    Requires(x * p + y * q == N),
    Modifies(x, q),
    Ensures(x * p + y * q == N)
  )
  x = x - y
  q = q - p // correct q = q + p
}

// At(x, 0) * p + y * At(q, 0) == N & x == At(x, 0) - y & q == At(q, 0) - p & x * p + y * q != N
// input:
//   At(x, 0) = 1  (for x)
//   At(q, 0) = 1  (for q)
//   p = 1 & y = 1 & N = 2
// we have:
//     1 * 1 + 1 * 1 == 2 & x == 1 - 1 & q == 1 - 1 & x * 1 + 1 * q != 2
// ->  2 == 2 & 0 * 1 + 1 * 0 != 2
// ->  2 == 2 & 0 != 2

// We have found a counterexample for the contract, a test case that exhibits the fault
// If the program is corrected as shown in the comment in the function, the test succeeds (as does the proof)

Linear Function Impure

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


// #Sireum #Logika
import org.sireum._

// linmap yields a * x + b for any a, x, and b
def linmap(a: Z, x: Z, b: Z): Z = {
  Contract(
    Ensures(Res == a * x + b)
  )
  return a * x + b
}

// given (x - b) % a == 0 revmap yields (x - b) / a for any a, x, and b
def revmap(a: Z, x: Z, b: Z): Z = {
  Contract(
    Requires(a != 0, (x - b) % a == 0),
    Ensures(Res == (x - b) / a)
  )
  return (x - b) / a
}

// compose yields x for any a, x, and b
def compose(a: Z, x: Z, b: Z): Z = {
  Contract(
    Requires(a != 0),
    Ensures(Res == x)
  )
  var y: Z = linmap(a, x, b)
  Deduce(|- (y == a * x + b))
  y = revmap(a, y, b)
  Deduce(|- (a != 0))
  Deduce(|- ((a * x + b - b) % a == 0))
  Deduce(|- (At(y, 0) == a * x + b))
  Deduce(|- (y == ((At(y, 0) - b) / a)))
  Deduce(|- (y == ((a * x + b - b) / a)))
  return y
}

Max Function Frame

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


// #Sireum #Logika
import org.sireum._

var z: Z = 0

def max(x: Z, y: Z) {
  if (x < y) {
    z = y
  } else {
    z = x
  }
}

Max Function Frame Contract

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


// #Sireum #Logika
import org.sireum._

var z: Z = 0

def max(x: Z, y: Z) {
  Contract(
    Requires(x > 0, y > 0),
    Modifies(z),
    Ensures(z == x | z == y, x <= z, y <= z)
  )
  if (x < y) {
    z = y
  } else {
    z = x
  }
}

Max Function Frame Contract Test

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


// #Sireum #Logika
import org.sireum._

var z: Z = 0

def max(x: Z, y: Z) {
  Contract(
    Requires(x > 0, y > 0),
    Modifies(z),
    Ensures(z == x | z == y, x <= z, y <= z)
  )
  if (x < y) {
    z = y
  } else {
    z = x
  }
}

// x > 0 & y > 0 & x < y & z == y & (z == x | z == y) & x <= z & y <= z
// satisfied by
//   input: x == 1 & y == 2
//   output: z == 2
// because
//   1 > 0 & 2 > 0 & 1 < 2 & 2 == 2 & (2 == 1 | 2 == 2) & 1 <= 2 & 2 <= 2
// ---
// x > 0 & y > 0 & x >= y & z == x & (z == x | z == y) & x <= z & y <= z
// satisfied by (x == y)
//   input: x == 1 & y == 1
//   output: z == 1
// because
//   1 > 0 & 1 > 0 & 1 >= 1 & 1 == 1 & (1 == 1 | 1 == 1) & 1 <= 1 & 1 <= 1
// ---
// x > 0 & y > 0 & x >= y & z == x & (z == x | z == y) & x <= z & y <= z
// satisfied by (x > y)
//   input: x == 2 & y == 1
//   output: z == 2
// because
//   2 > 0 & 1 > 0 & 2 >= 1 & 2 == 2 & (2 == 2 | 2 == 1) & 2 <= 2 & 1 <= 2

Max Function Pure

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


// #Sireum #Logika
import org.sireum._

@pure def pure_max(x: Z, y: Z): Z = {
  if (x < y) {
    return y
  } else {
    return x
  }
}

def max(x: Z, y: Z): Z = {
  if (x < y) {
    return y
  } else {
    return x
  }
}

val x = randomInt()
val y = randomInt()

val z = max(x, y)
Deduce(|- (z == pure_max(x, y)))

Max Function Pure Contract

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


// #Sireum #Logika
import org.sireum._

def max(x: Z, y: Z): Z = {
  Contract(
    Requires(x > 0, y > 0),
    Ensures(Res == x | Res == y, x <= Res, y <= Res)
  )
  if (x < y) {
    return y
  } else {
    return x
  }
}

Max Function Pure Contract Test

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


// #Sireum #Logika
import org.sireum._

def max(x: Z, y: Z): Z = {
  Contract(
    Requires(x > 0, y > 0),
    Ensures(Res == x | Res == y, x <= Res, y <= Res)
  )
  if (x < y) {
    return y // "Res = y"
  } else {
    return x // "Res = x"
  }
}

// x > 0 & y > 0 & x < y & Res == y & (Res == x | Res == y) & x <= Res & y <= Res
// satisfied by
//   input: x == 1 & y == 2
//   output: Res == 2
// because
//   1 > 0 & 2 > 0 & 1 < 2 & 2 == 2 & (2 == 1 | 2 == 2) & 1 <= 2 & 2 <= 2
// ---
// x > 0 & y > 0 & x >= y & Res == x & (Res == x | Res == y) & x <= Res & y <= Res
// satisfied by (x == y)
//   input: x == 1 & y == 1
//   output: Res == 1
// because
//   1 > 0 & 1 > 0 & 1 >= 1 & 1 == 1 & (1 == 1 | 1 == 1) & 1 <= 1 & 1 <= 1
// ---
// x > 0 & y > 0 & x >= y & Res == x & (Res == x | Res == y) & x <= Res & y <= Res
// satisfied by (x > y)
//   input: x == 2 & y == 1
//   output: Res == 2
// because
//   2 > 0 & 1 > 0 & 2 >= 1 & 2 == 2 & (2 == 2 | 2 == 1) & 2 <= 2 & 1 <= 2

Max Function Pure Deduce

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


// #Sireum #Logika
import org.sireum._

@pure def pure_max(x: Z, y: Z): Z = {
  Contract(
    Requires(x > 0, y > 0),
    Ensures(Res == x | Res == y, x <= Res, y <= Res)
  )
  if (x < y) {
    return y
  } else {
    return x
  }
}

var z: Z = randomInt()

def impure_max(x: Z, y: Z) {
  Contract(
    Requires(x > 0, y > 0),
    Modifies(z),
    Ensures(z == x | z == y, x <= z, y <= z)
  )
  if (x < y) {
    z = y
  } else {
    z = x
  }
}

val x = randomInt()
assume(x > 0)
val y = randomInt()
assume(y > 0)

impure_max(x, y)

Deduce(|- (z == pure_max(x, y)))

Two Square Contract Test Fault

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


// #Sireum #Logika
import org.sireum._

var x: Z = randomInt()
var y: Z = randomInt()

def tsq() {
  Contract(
    Modifies(x, y),
    Ensures(x >= 0, y >= 0)
  )
  x = x * x
  y = y + y // correct: y = y * y
  if (x < y) {
    y = y - x
  } else {
    x = x - y
  }
}

// Unsatisfiable "(At(x, 1) < At(y, 1))"
// At(x, 1) == At(x, 0) * At(x, 0) &
// At(y, 1) == At(y, 0) + At(y, 0) &
// (At(x, 1) < At(y, 1)) &
// (At(x, 1) < At(y, 1)) -> (x == At(x, 1)) &
// (At(x, 1) < At(y, 1)) -> (y == At(y, 1) - x) &
// y < 0

// Branch with counterexample "!(At(x, 1) < At(y, 1))"
// At(x, 1) == At(x, 0) * At(x, 0) &
// At(y, 1) == At(y, 0) + At(y, 0) &
// !(At(x, 1) < At(y, 1)) &
// !(At(x, 1) < At(y, 1)) -> (y == At(y, 1)) &
// !(At(x, 1) < At(y, 1)) -> (x == At(x, 1) - y) &
// y < 0

// Compare symbolic execution!

Summary

We have discussed pure and impure functions.

We have introduced contracts with:

Pre-conditions,
Post-conditions, and
Frames

We have discussed how to derive test cases from:

Specifications (resp. function contracts) and
Implementation (resp. function bodies – and contracts)

We have analysed programs that contain faults and derived test cases for those.